一、题目

前段时间有粉丝问了一道题，题目如下：

如图，已知在正方形ABCD中，有一点O，AO=7，CO=9，BO=4，求正方形ABCD的面积。

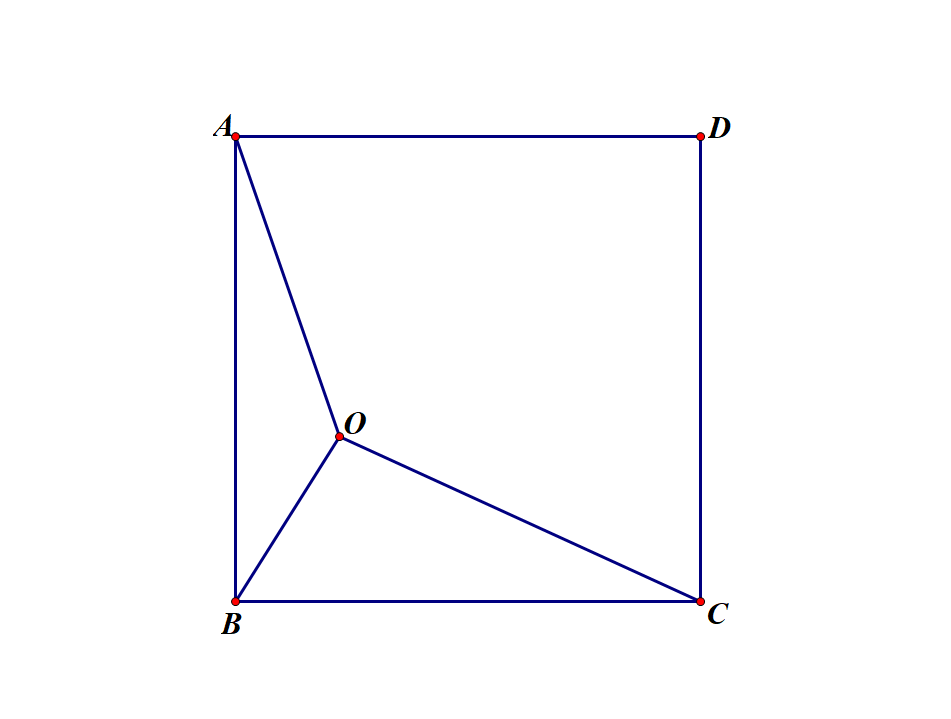
二、分析

要求正方形的面积，只要求出正方形边长，题目中已知条件，除了明确给出的3条线段长外，△AOB和△BOC还存在边相等、角互余的隐含条件，据此，容易想到把其中一个三角形旋转90°，使俩等边重合，进而构造出一个含直角且四边都已知的四边形，求它的对角线长。

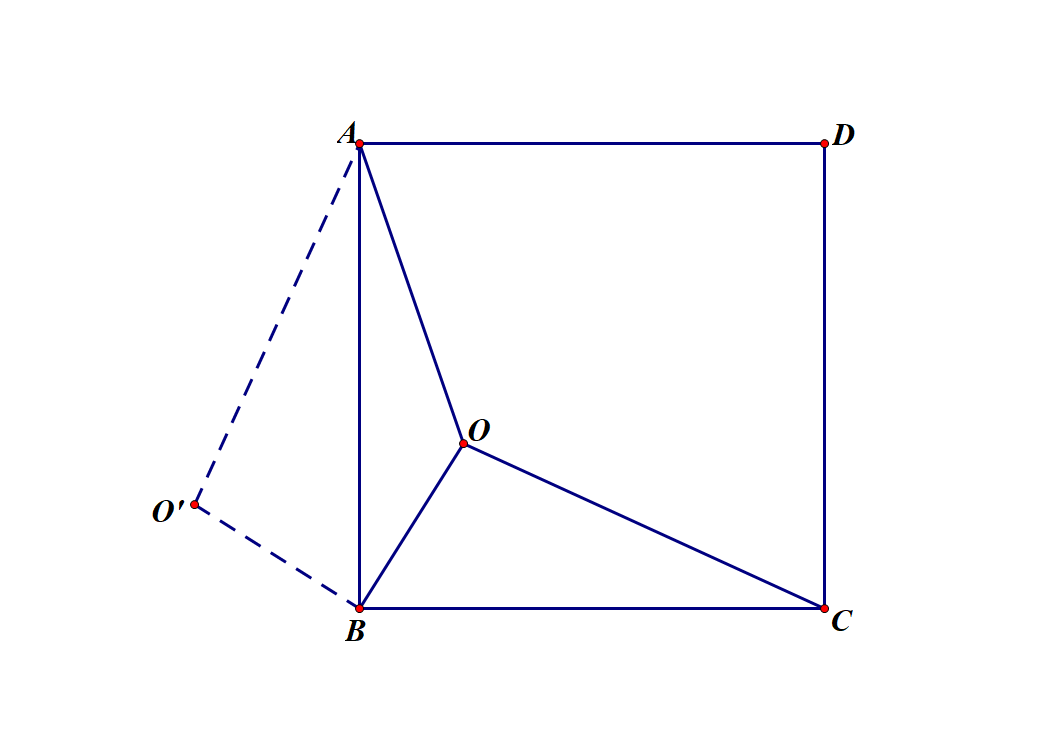
如图，把△BOC绕点B逆时针旋转90°至△BO'A，则O'B=OB=4，O'A=OC=9，∠O'BO=∠ABC=90°.

条件不足，继续拓展已知条件，旋转出等腰，旋转90°出等腰直角三角形

连接OO'，由勾股定理可得 OO'=4√2

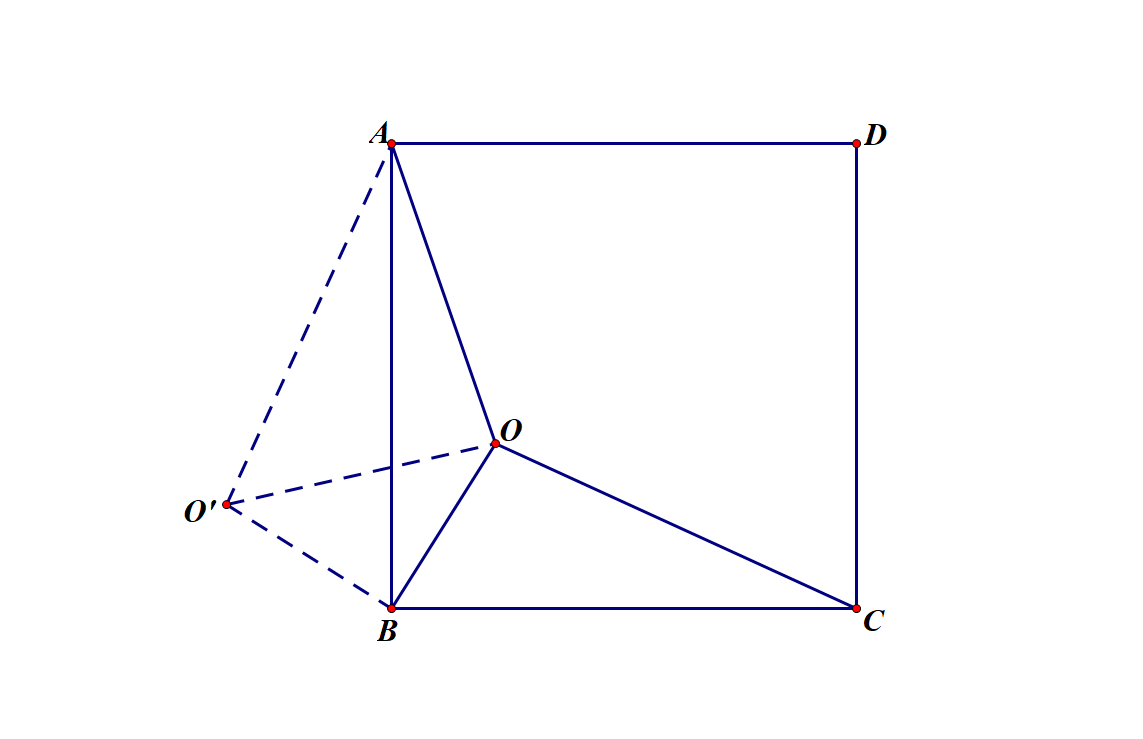
O'A=9，OA=7，OO'=4√2

由勾股定理逆定理可判断 △AOO'为直角三角形，∠AOO'=90°

∴∠AOB=135°

现在又得到了一个特殊角，构造特殊三角形，利用勾股定理即可求得AB

过点B作BE⊥AO，交AO延长线于点E

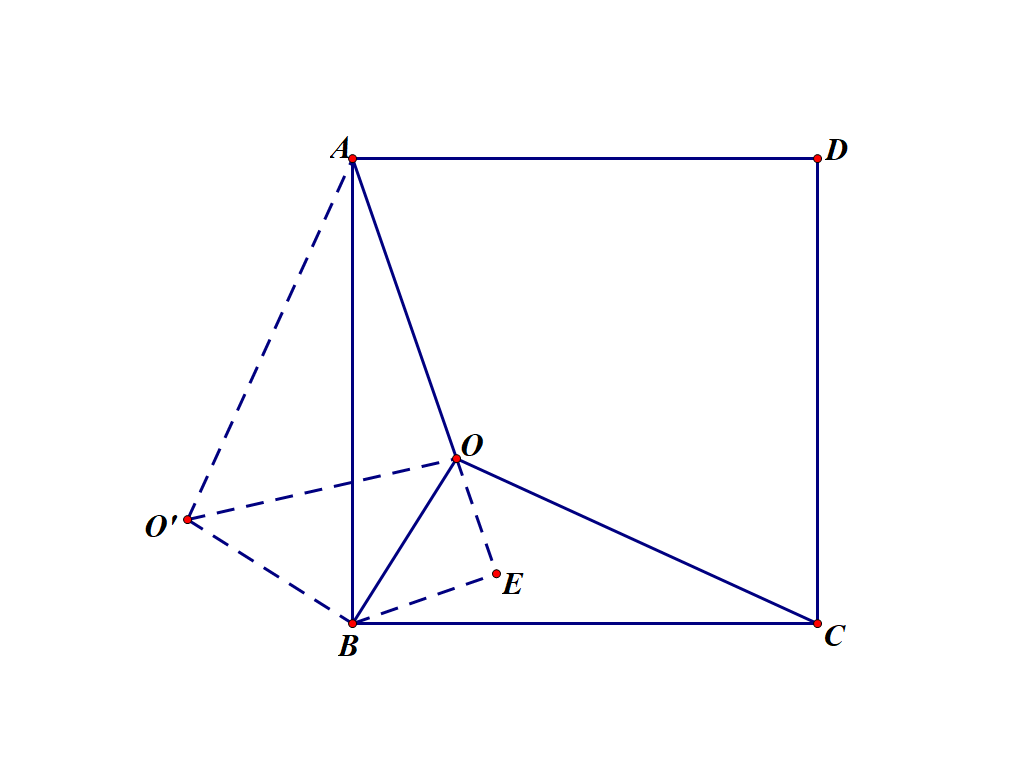
则△BOE为等腰直角三角形

BE=OE=OB/√2=2√2，AE=AO+OE=7+2√2

在RT△ABE中，由勾股定理可得

AB^2=65+28√2

∴四边形ABCD的面积为65+28√2

另解

这道题也可以利用坐标法求解，列式非常简单，但是计算量比较大，对计算能力要求比较高。

以点B为坐标原点，BC所在直线为x轴，AB所在直线为y轴建立平面直角坐标系

设A(0,a)，C(a,0)，O(x,y)

由两点间距离公式可得3个二元二次方程

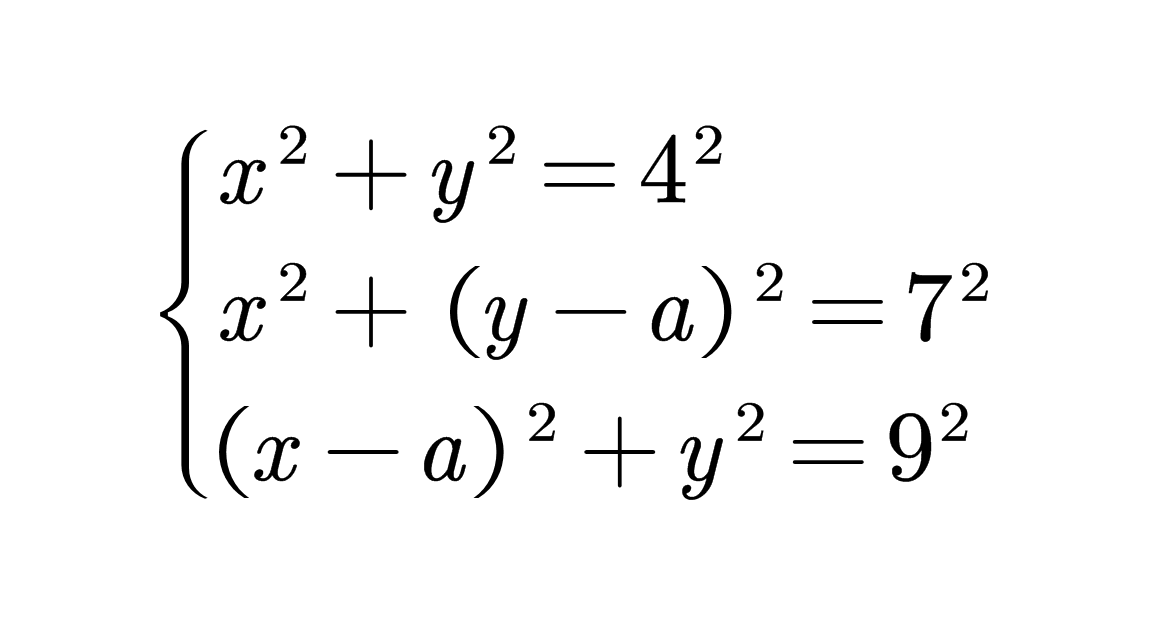
也可解得a^2=65+28√2

1、本题的特殊性在于，旋转后构成的四边形恰好可分为两个直角三角形，进而得到∠AOB=135°这个特殊角，进而构造特殊直角三角形由勾股定理求得线段长。

2、由方法二可知，即使△AOO'不是直角三角形，同样可解。

3、对比两种方法，方法一充分利用了图形的性质来解题，计算很简单，但必须步步为营；方法二列式很简单，无需考虑图形的具体性质，但是计算量很大。平时解题时，一般先从图形特点出发，利用图形性质来解题，当题目较复杂，不知该如何下手时，可尝试坐标法。