一.概念描述
现代数学:认识底面积之前,我们要先了解底面的概念。在一个多面体中,如果有两个面互相平行而其余每相邻的两个面的交线互相平行,则这样的多面体称为棱柱。依底面为三角形、四边形直至n边形,而将棱柱分别称为三棱柱、四棱柱直至n棱柱。棱柱中互相平行的两个面称为棱柱的底面,其余各面称为棱柱的侧面。底面的面积即底面积。
小学数学:小学数学教材是这样定义的:
①2006年人教版教材五年级下册的第43页指出:长方体或正方体底面的面积,叫作底面积。
②2006年北京版教材第10册的第17页指出:长乘宽的积就是长方体的底面积。
③2005年北师大版教材五年级下册的第47页以直观形式呈现:给出了长方体和正方体的透视图,用阴影标出底面,并指出阴影部分的面积是长方体和正方体各图形底面的面积,称为底面积。
二.概念解读
底面是棱柱中互相平行的两个面,也就是在棱柱中有上、下两个底面。
在小学阶段主要认识长方体、正方体、圆柱、圆锥这四个立体图形。在长方体中相对的面互相平行.共有三组,且习惯上把下面称为底面,底面的形状是长方形或正方形。底面的大小最多有三种情况(长乘宽、长乘高、高乘宽),有两个相对面是正方形的长方体,底面的大小就有两种情况。长方体摆放的方法不同,底面和侧面也会随之变化,因此长方体的底面和侧面是相对而言的。
圆柱的两个底面是圆形,圆锥只有一个圆形的底面,它的另一个底面可以想象成这个底面缩成一个点。
小学阶段常见的棱柱的底面有长方形、正方形、三角形、梯形、圆以及正n边形,计算底面积也就是计算这些平面图形的面积。
《数学辞海·第一卷》第182页指出:几何学的起源几乎直接联系着面积的计算,从计算最简单的矩形面积到精确计算任意形状的图形面积,经历了漫长的历史发展过程。从现有资料看,许多文明古国都有用长乘宽计算矩形面积的记载,这是最原始的面积定理,而其他多边形的面积都是通过矩形面积推导出来的,如古埃及人用公式((a+c)/2)·((b+d)/2)来近似计算四边形顺次为a,b,c,d的四边形的面积,并对此公式做了推论,让四边形的一边为零,而得三角形面积的近似公式:c/2·(a+b)/2。
公元前5世纪,希俄斯的希波克拉底就提出月形定理,他把两个月形面积转化为一个直角三角形的面积。1世纪,海伦在几何学面积方面已有许多研究成果,他以几何形式推算出求三角形面积的海伦公式:
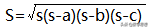
其中S为三角形面积,a,b,c是三角形的边长,s是三角形的周长之半。6世纪前后,婆罗摩笈多在他的著作中给出了与海伦公式形式类似的圆内接四边形的面积公式:
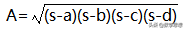
其中A为圆内接四边形的面积,a,b,c,d是四边形周长的一半。刘徽用割补数计算出三角形面积、梯形面积的精确公式,蔡久韶独立发现了与海伦公式等价的三角形面积公式---三斜求积公式:
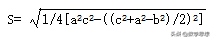
其中S为三角形的面积,三边a,b,c分别成为大斜、中斜、小斜(a>b>c>0)。
在计算图形面积的历史发展过程中,极限思想早已孕育和萌发。公元前3世纪,阿基米德就运用穷竭法求出了抛物弓形面积及直线与螺线围成的区域面积,这是数学史上最早的极限思想的体现。公元前3世纪刘徽用割圆术求圆面积的方法、12世纪印度人用“印度圆”求圆面积的方法、开普勒用无限个微小三角形求圆面积的方法等,都是极限方法的雏形,为17世纪微积分的创立打下了基础。至17世纪后,才确立了用特定数学结构的和式极限---定积分计算图形的面积。
三.教学建议
(1)从动态的角度丰富学生对底面积的认识
小学阶段是结合长方体、正方体等实物模型,让学生直观认识底面积。棱柱的认识是培养学生空间观念的重要组成部分,对底面积的深刻理解有助于学生建构知识,发展空间观念。教学时,教师可以从动态的角度丰富学生对底面积的认识。这主要有以下几种角度。
①直截:用垂直于柱的母线的平面去截柱体,所得的截面面积与底面积相等。
②射影:把长方形、三角形、正多边形、圆等平面图形进行正射影,所形成的射影面是直棱柱的底面,两个底面之间的距离是棱柱的高。
③平移:把长方形垂直于平面并沿平面位移,由起点到终点这条边所扫过的部分就是这个棱柱的底面。
④旋转:一个长方形绕其一边旋转一周而成为直圆柱,长方形中垂直于轴的边旋转而成的圆面成为圆柱的底面。直角三角形绕其一直角边旋转一周而成为圆锥,垂直于轴的边旋转而成的面是圆锥的底面。
(2)以底面积为纽带,沟通知识间的联系,掌握计算棱柱体积的方法,形成知识体系
①找共同点,沟通联系。
在学完长方体的体积V =abh和正方体的体积V=a的三次方之后,引导学生观察思考:长方体体积中“长×宽”计算的是哪个面的面积?正方体体积中“棱长×棱长”计算的是哪个面的面积?这两个公式可以概括成一个公式吗?学生讨论后用课件演示:这两个公式分别求的是长方体的底面积和正方体的底面积。它们都是用“底面积x高”。因此长方体和正方
体的体积可以用V=sh来概括。
②迁移知识,建构体系。
教学圆柱体积时,教师可以首先引导学生回顾长方体、正方体的体积是“底面积×高”,然后引导学生探索圆柱体积计算方法。学生在老师的启发下,借助圆形面积公式推导的活动经验和转化方法,将圆柱的底面等分后再沿着高切开,把圆柱拼成近似的长方体,得出圆柱体积等于“底面积×高”。这一探索过程沟通了长方体与圆柱的关系,计算它们的体积都可以用“底面积×高”。在此基础上,还可以根据V=sh拓展提升,如让学生求出底面为三角形、梯形、正六边形的直棱柱体积,并拓展延伸,以底面积为主线帮助学生建构知识。
四.推荐阅读
(1)《实用数学手册》(叶其效、沈永欢,科学出版社,2006)
该书第26页从棱柱的角度介绍了底面,揭示了底面和棱柱的关系还介绍了侧面、侧棱和高。
(2)《数学大辞典》(王元,科学出版社,2010)
该辞典不仅从棱柱的角度介绍底面和侧面,还从旋转的角度介绍了圆柱的形成过程,从而介绍底面。










